1 When factored, the expression x3 – 36x is equivalent to
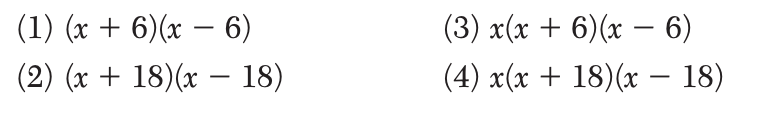
Solution: First, we need to factor out the greatest common factor. In this case, it is x. We get x(x2−36)
Next we recognize the difference of squares, we get x(x-6)(x+6). Choice 3 is the correct answer.
2 Which equation represents the line that passes through the points (-1,8) and (4,-2)?

Solution: Let’s use the slope intercept form y=mx+b where m is slope and b is y-intercept. To get slope we use the formula m=(y2−y1)/(x2−x1) = (−2−8)/(4–1) = -2.
Next we use y−y1=m(x−x1), plugging in one of the points such as (-1, 8) and slope m=−2.
We get y−8=−2(x+1)
y−8=−2x−2
y=−2x+6
Choice 1
3 A geometric sequence is shown below. 1/2 , 2, 8, 32, …
What is the common ratio?

Solution: To find the common ratio in a geometric sequence, we need to divide any term by the previous term. 2 divided by 1/2 is equal 4. Similarly 8 divided by 2 is 4 and so on. Choice 4 is the correct answer.
4 What is the constant term of the polynomial 2x3– x + 5 + 4x2?
(1) 5 (3) 3 (2) 2 (4) 4
Solution: The constant term is the term without any variables, which is 5 in this case. Choice 1 is the correct answer.
5 A landscaping company charges a set fee for a spring cleanup, plus an hourly labor rate. The total cost is modeled by the function C(x) = 55x + 80. In this function, what does the 55 represent?
(1) the set fee for the cleanup
(2) the hourly labor rate for a cleanup
(3) the profit earned by the company for one cleanup
(4) the number of hours of labor required for one cleanup
Solution: We can notice that 55 is times X which means that this is an hourly rate. X is the number of hours. 80 is without x and would be the set fee. Choice 2 is the correct answer.
6 Which expression is equivalent to (5x2 – 2x + 4) – (3x2 + 3x – 1)?

Solution: Distribute the minus sign to the second group: (5x2 – 2x + 4) – 3x2 – 3x +1
Combine like terms: 2x2-5x + 5. Choice 2 is the correct answer.
7 A system of inequalities is graphed on the set of axes below.

Solution: A solution is within the region that is shaded for both lines. Choice 4 is the correct answer.
8 In an arithmetic sequence, the first term is 25 and the third term is 15. What is the tenth term in this sequence?
(1) -20 (3) 70 (2) -25 (4) 75
Solution: An arithmetic sequence has the following formula: an=a1+(n−1)d where an is the nth term and a1 is the first term. We get 15=25+(3-1)d
d= -5
Now, we can plug in d and first term to find the tenth term
an = 25+(10-1)(-5) = -20. Choice 1 is the correct answer
9 When the formula p = 2l + 2w is solved for w, the result is

Solution: Lets solve p = 2l + 2w. We need to isolate w. We get p-2l= 2w. Then we need to divide by 2 and get (p-2l)/2=w. Choice 2 is the correct answer.
10 Market Street Pizza kept a record of pizza sales for the month of February. The results are shown in the table below.
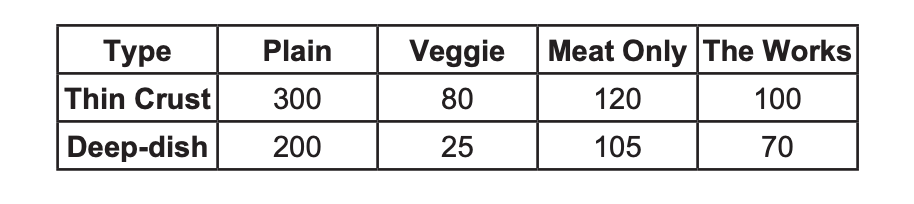
Of all the pizzas sold in February, what percent were plain, deep-dish pizzas? (1) 20% (3) 40% (2) 30% (4) 50%
Solution: First, we need to find the number that represents plain, deep-dish pizzas which is 200. Next, we have to divide it by the total number of pizzas and multiply by 100% to find percent. We will add all of the numbers in the table to find the total number. We get 1000 pizzas.
% = (200/1000)*100% = 20%. Choice 1 is the correct answer.
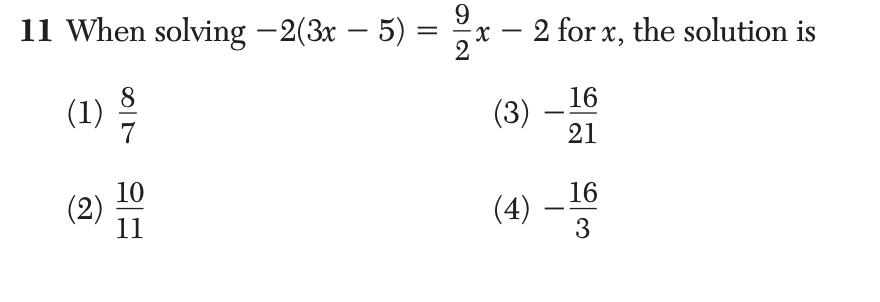
Solution: First we can multiple both sides of the equation by 2 to get rid of the denominator. We get: -4(3x-5)=9x-4.
Next we can open parenthesis and then group like terms with one another.
-12x+20 = 9x-4
-12x-9x = -4-20
-21x = -24
x= -24/-21 = 8/7. Choice 1 is the correct answer
12 The expression x2a + b is equivalent to

Solution: The expression x2a + b is equivalent to xa*xa+b. Choice 3 is the correct answer
13 The inputs and outputs of a function are shown in the table below.
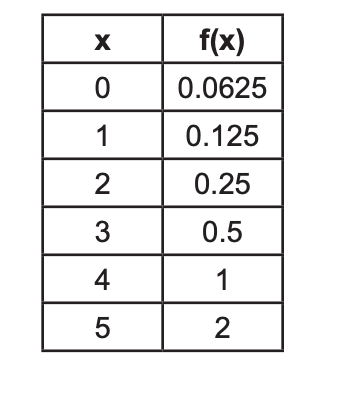
This function can best be described as
(1) linear (3) exponential (2) quadratic (4) absolute value
Solution: From x = 0 to 1: the output doubles (0.0625 → 0.125). From x = 1 to 2: 0.125 → 0.25 (doubles again). Then: 0.25 → 0.5 → 1 → 2 (keeps doubling). This is an exponential function. Choice 3 is the correct answer.
14 Stephanie is solving the equation x2 – 12 = 7x – 8.
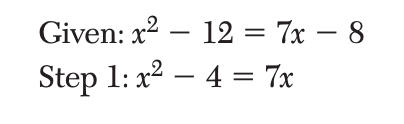
(1) associative property (3) distributive property (2) commutative property (4) addition property of equality
Solution: This step uses the Addition Property of Equality, which states that you can add the same value to both sides of an equation without changing the equality. Choice 4 is the correct answer
15 What is the sum of 8 √3 and √3 ?

Solution: To find the sum of 8√3+√3, you simply add the like terms (they both have the same radical part, (8+1)√3 = 9√3. Choice 4 is the correct answer.
16 The dot plots below represent test scores for 20 students on a math test.
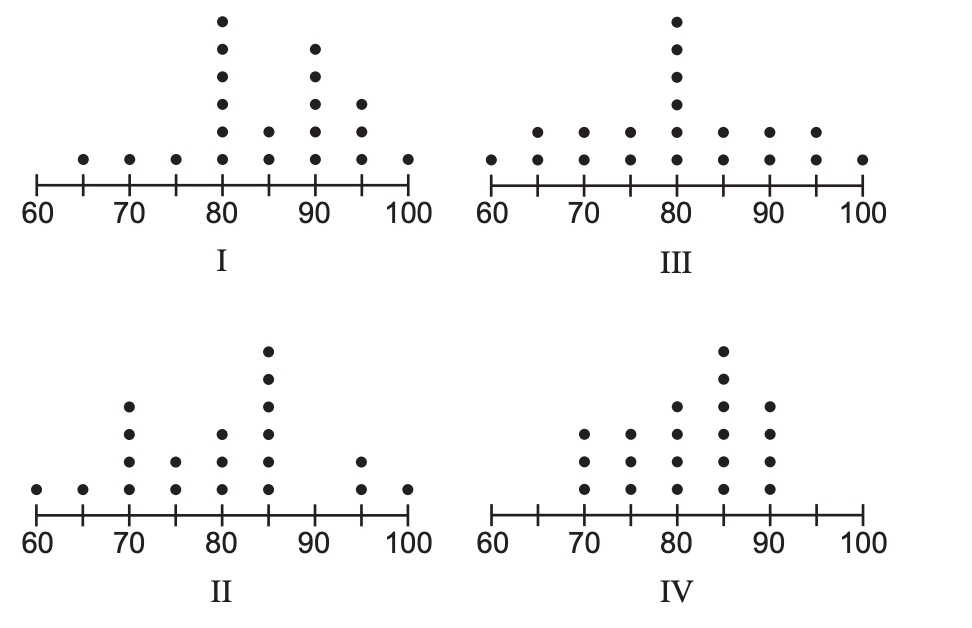
The mode for this math test is 80 and the median is 85. Which dot plot correctly represents this data?
(1) I (3) III (2) II (4) IV
Solution: We are told: Total students = 20 Mode = 80 (most frequent value) Median = 85 (middle value when data is ordered)
Let’s first look at the most frequent value (the one with most dots.). We can eliminate choices 2 (mode is 85) and 4 (mode is 85). Median must be the 10th point. Looking at plot 3, 10th point is 80, eliminating choice 3. Choice 1 is the correct answer.
17 A function is graphed on the set of axes below.
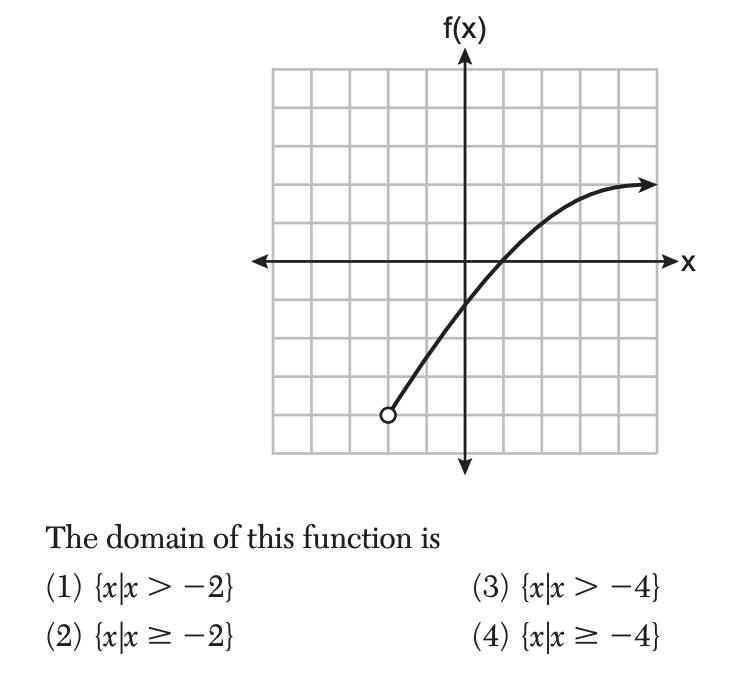
Solution:From the graph, the function starts at x=−2x=−2 with an open circle, meaning x=−2x=−2 is not included in the domain.
The curve extends indefinitely to the right. So, the domain is:{x∣x>−2}. That corresponds to option (1).
18 Which ordered pair is a solution to the equation
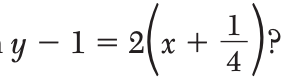

Solution: One way to solve this question is to plug in x value (first number) from each answer choice to see if it corresponds to the correct y value. Choice 2 is the correct answer choice.
19 Elena’s fastest time for the 50-meter dash is 7 seconds. She wants to know how fast this is in inches per minute. Which expression can Elena use for a correct conversion?

Solution: We are told that Elena runs 50 meters in 7 seconds and that is what we need to start with, eliminating choices 1 and 2. Next, to convert seconds to minutes, we will put 60 seconds on top and 1 minute on the bottom. Next, to convert meters to inches, meters need to go on the bottom (to get crossed out) and inches on top. Choice 4 is the correct answer choice.
20 The table below shows the highest temperatures recorded in August for several years in one town.
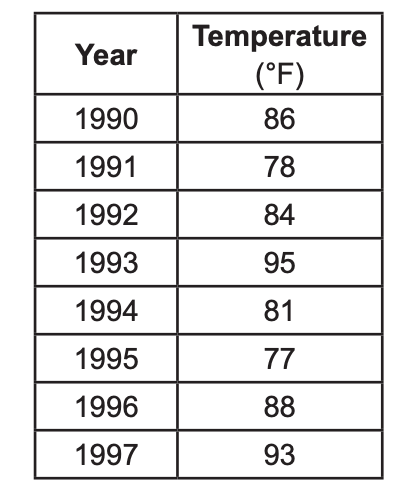
The interquartile range of these data is
(1) 7 (3) 11 (2) 10 (4) 18
Solution: Let’s find the interquartile range (IQR), which is: IQR=(Q3−Q1)I
Step 1: Order the temperatures from least to greatest
77, 78, 81, 84, 86, 88, 93, 95
Step 2: Find Q1 and Q3 There are 8 data points.
Q1 = median of the lower half (first 4 numbers): 77, 78, 81, 84
Q1=(78+81)/2=159/2=79.5
Q3 = median of the upper half (last 4 numbers): 86, 88, 93, 95 Q3=(88+93)/2=181/2=90.5
Step 3: Calculate IQR IQR=90.5−79.5=11, Choice 3 is the correct answer choice.
21 The function f(x) = x2 is multiplied by k, where k <- 21. Which graph could represent g(x) = kf(x)?
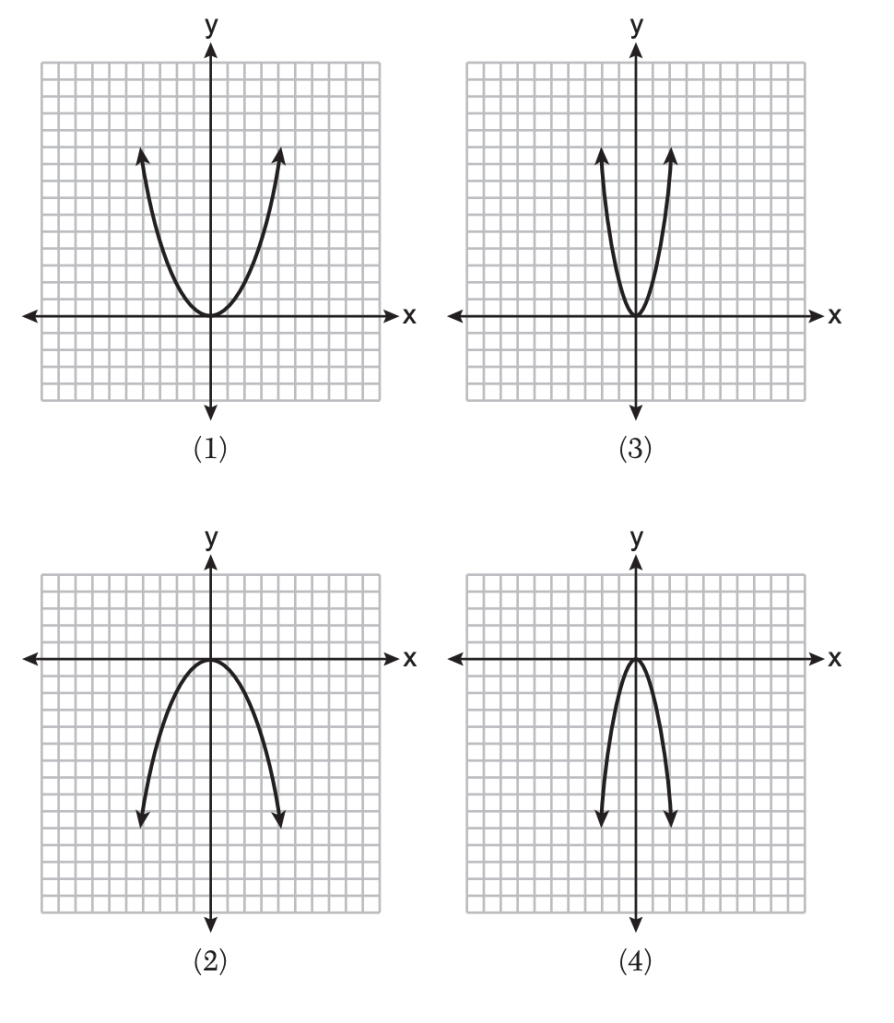
Solution: k<−21 means k is negative and has a large magnitude.The negative sign flips the parabola upside down (opens downward).The large magnitude makes it very narrow (steeper). Choice 4 is the correct answer.
22 Which graph is the solution to the inequality 6.4 – 4x ≥ -2.8?
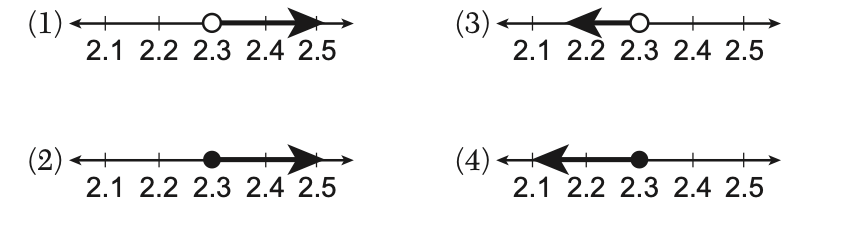
Solution: First we need to isolate x in the inequality,
6.4 – 4x ≥ -2.8
-4x≥ -2.8-6.4
-4x≥-9.2
x≤2.3 (reverse the sign because we divided by a negative number).
Choice 4 is the correct answer because the circle is shaded in because of the equal sign and x is less than or equal to 2.3
23 The number of fish in a pond is eight more than the number of
frogs. The total number of fish and frogs in the pond is at least 20.
If x represents the number of frogs, which inequality can be used to
represent this situation?

Solution:Let x represent the number of frogs in the pond. Since there are eight more fish than frogs, the number of fish is x+8. The total number of frogs and fish is then x+(x+8)==2x+8. Because the total number of animals is at least 20, we write the inequality 2x+8≥20 to represent this situation. Choice 2 is the correct answer choice.
24 Which graph below represents a function that is always decreasing
over the entire interval -3 < x <3?
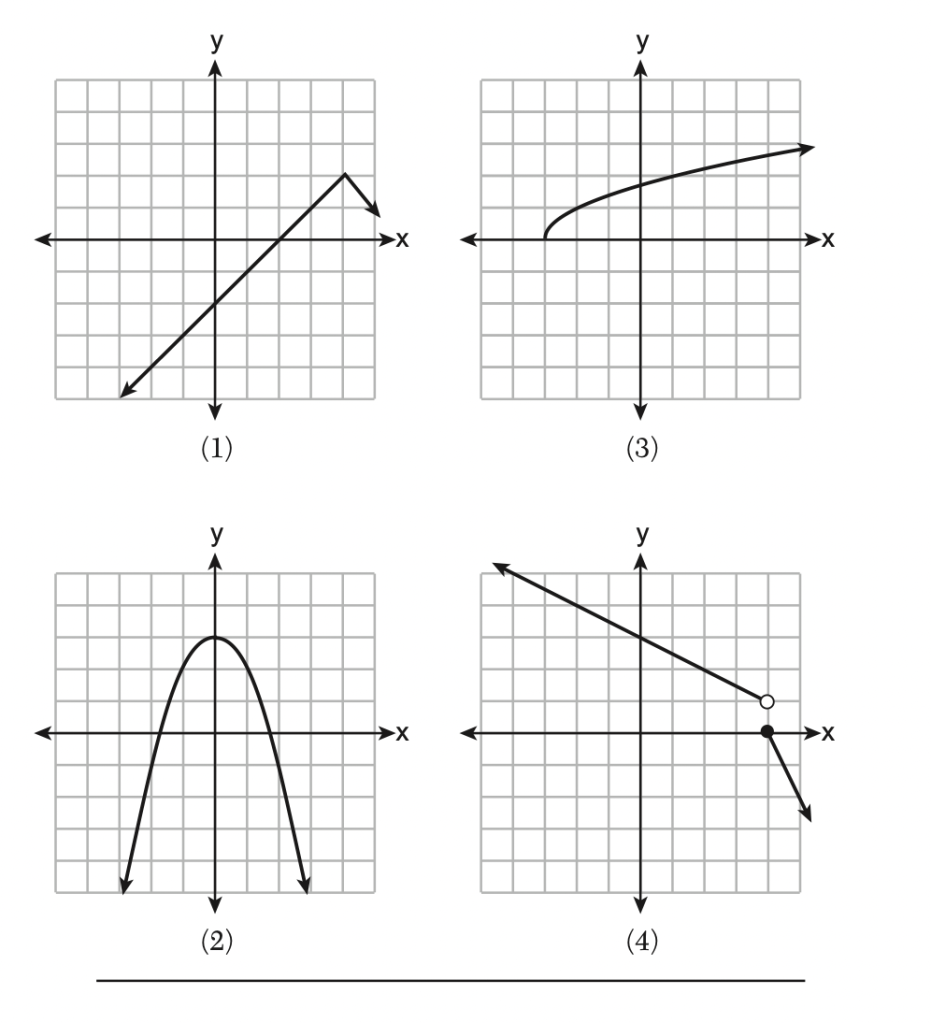
Solution: A function that is always decreasing over −3<x<3means: The slope must be negative everywhere in that interval. As x increases, f(x) must continuously decrease. There can’t be any turning points (no going up then down). Choice 4 is the correct answer choice.